
In QCM instrument specifications and in experimental descriptions in publications, there is always a reference to the fundamental frequency of the QCM crystal. Typically, it is 5 – 10 MHz, but it can also be 15 MHz, 30 MHz or even higher. How come the fundamental frequency is always mentioned? Does it really matter? Here we sort out the details and explain the significance of the QCM fundamental frequency in a measurement situation.
The QCM fundamental frequency, f0, refers to the lowest frequency where the crystal can be excited to resonance. Several key characteristics are linked to this specific frequency, such as
The fundamental frequency is inversely proportional to the thickness, h, of the crystal disk, eq. (1). The higher the fundamental frequency, the thinner the crystal. For example, a 5 MHz QCM crystal will have a thickness of ~334 um, and a 10 MHz crystal will be half that, and have a thickness of ~167 um.
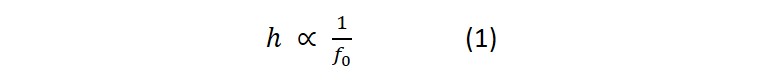
According to the Sauerbrey equation, the mass sensitivity, C, of a QCM is inversely proportional to the square of the fundamental frequency, eq. (2). In theory, this means that the higher the fundamental frequency, the better the sensitivity, i.e., smaller mass changes can be resolved. For example, 5 MHz and 10 MHz crystals have theoretical mass sensitivities of 17.7 ng/(cm2∙Hz) and 4.4 ng/(cm2∙Hz) respectively. This means that a 10 MHz crystal will have a four times larger frequency response to a given surface mass compared to a 5 MHz crystal.
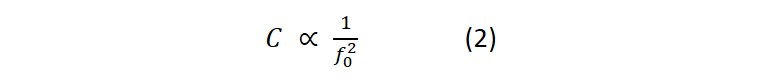
From a sensitivity perspective, a high fundamental frequency might seem to be something to strive for. In practice, however, it is not so simple. There are several aspects that make a high fundamental frequency less palatable.
First, as already mentioned, the higher the fundamental frequency, the thinner the crystal, and at some point, the crystal will be so thin and fragile that it will be impractical to handle1.
Second, the higher the frequency, the higher the measurement noise. There are several reasons for this. One is that the imperfections in flatness and thickness from manufacturing, that cannot completely be avoided, will have a larger negative impact on the resonance quality the thinner the crystal is. Also, noise levels go up with frequency in drive and measurement electronics, contributing to measurement uncertainty.
One might think then, considering the above, that a thick sensor (i.e., low fundamental frequency) would be ideal. However, it is not that simple. All crystals have defects, such as dislocations and impurities. These defects will have a negative impact on resonance quality and the fewer the better. From this perspective, one would favor thin crystals that have less defects compared to a thick crystal. We, therefore, as usual, end up in a trade-off when it comes to sensor thickness.
To conclude, a high theoretical sensitivity does not directly correlate with a better mass detection limit. More important are aspects such as signal-to-noise ratio and long-term stability to predict how good your measurement will be.
A third parameter related to the resonance frequency is the sensing depth, δ, which is inversely proportional to the square root of the resonance frequency, eq. (3). The lower the resonance frequency, the thicker the layer that can be sensed. For example, the penetration depth of the shear wave in water at room temperature for 5, 10 and 30 MHz crystals are ~250 nm, ~180 nm, and ~100 nm, respectively.
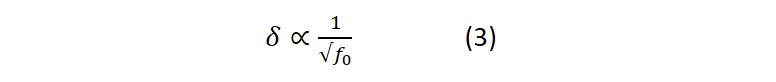
Finally, a comment on the overtones. To perform full viscoelastic modeling of the QCM data, information on frequency and dissipation from multiple harmonics is needed. For traditional QCM, where the crystal is oscillating in the thickness-shear mode, only odd harmonics can be excited, i.e., the overtones will be odd multiples of the fundamental, eq. 4. For example, to access 7 harmonics with a 5 MHz crystal, you need to be able to excite the crystal up to 65 MHz. The corresponding frequencies for 10 MHz and 30 MHz crystals would be 130 MHz, and 390 MHz respectively, where, as already mentioned, the impact of the noise will more and more noticeable as the frequency increases.
As discussed above, the QCM fundamental frequency is related to several properties and performance parameters such as crystal thickness, theoretical mass sensitivity, sensing depth and the magnitude of the overtone frequencies.
The parameter that gets the most attention is the theoretical mass sensitivity. Since this mass sensitivity increases with the fundamental frequency, it is intuitive to aspire for a high fundamental. However, the useful mass sensitivity, i.e., the sensitivity obtained in a real measurement situation, does not necessarily correlate with the theoretical value, as this can be significantly impaired by increasing noise as well as limitations of the hardware and electronics, which reduces how much of the crystal capacity that can be utilized in the actual measurement output.
Download the guide to read more about the QCM fundamental frequency and which other key aspects of a QCM specification that will have an impact on the performance of the instrument.
1 There are ways around this hurdle. For example, there are crystal designs where a thin sensing area is milled in a thick piece of crystal, which then acts as a mechanical support for the fragile sensing area.
Editor’s note: This post was originally published in December 2018 and has been updated for comprehensiveness
Read the guidelines on how to decide which QCM instrument will be the most suitable for your needs
Read about what single-harmonic and multi-harmonic QCM-D means and what the difference is between these instruments.
Learn about the difference between the theoretical QCM sensitivity and the sensitivity which is relevant in a measurement situation.
Read about the piezoelectric effect and how piezoelectricity arises
QSense Omni is designed to offer cutting-edge QCM-D performance in modular setup-configurations based on user needs
To quantify the QCM mass you can use either the Sauerbrey equation or viscoelastic modelling. Learn what happens if you use the wrong approach.
Learn more about the different QCM:s and when to use which one.
QSense Omni is designed to minimize the user knowledge required to produce high-quality QCM-D data.
The quality of the data produced by an analytical instrument is crucial and noise and drift play a significant role in determining the outcome.
