If you are familiar with QCM-technology, you have most likely also encountered the so-called Sauerbrey equation. So, what is this equation, and when should it be used?
The ability of QCM technology to measure mass changes originates in the discovery of the relation between the resonance frequency and the mass. The relation was formulated in an equation in 1959 by Günter Sauerbrey, at the time a Ph.D. student in Berlin. The equation is a linear relationship between the resonance frequency of an oscillating quartz crystal and mass changes, Eq. 1.

In practice, this equation can be used to calculate the mass of thin layers added to a QCM crystal surface. By inserting the resonance frequency change, ∆f, that results from the layer addition, into Eq. 1, you will get the mass, ∆m, of the added layer. The constant, C, which is the so-called the mass sensitivity constant, is related to the properties of quartz. For example, for a 5 MHz crystal, C equals 17.7 ng/(cm2∙ Hz). The parameter n in the equation is the number of the harmonic, which can be an odd number 1, 3 ,5 ,7 ,… etc.
The linear frequency-mass relation described by eq. 1, is based on the behavior of a pure quartz crystal, where a crystal of thickness h (and mass m) will have a certain resonance frequency, f (Fig. 1, left).If similar enough to a “pure-quartz” scenario, the scenario where a layer of material, different from quartz, is added to the surface, can be approximated with a thicker crystal.
The model assumes that the added layer can be approximated to be a part of the oscillating crystal itself, which means that the crystal will now have the thickness h + Δh (Fig. 1, right). For this assumption to be valid, the layer on the sensor must be thin, rigid and firmly attached to the crystal surface, and the equation should only be used when these conditions are fulfilled. If the layer on the sensor is soft, thick or not coupled to the surface, the equation is not valid. In these situations, the model will fail, and the mass calculated with the Sauerbrey equation will be underestimated.
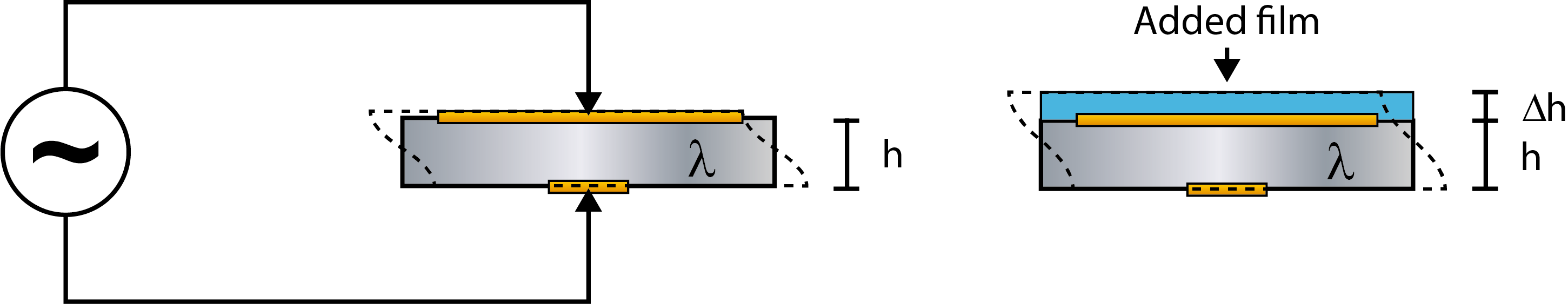 Figure 1. (Left) Schematic illustration of a quartz crystal, of thickness h and mass m, excited to resonance by the application of an alternating voltage.
Figure 1. (Left) Schematic illustration of a quartz crystal, of thickness h and mass m, excited to resonance by the application of an alternating voltage.
(Right) An oscillating crystal with added mass. Now the thickness is h + Δh and the mass is m + Δm.
If you are using a QCM setup that measures the energy loss, e.g. QCM-D, or a setup that has the capability of measuring at multiple harmonics, the applicability of the Sauerbrey equation can be identified by looking at the raw data. The raw data will reveal applicability either by showing a low energy loss or overlapping overtones, if those are measured. If the Sauerbrey equation is not applicable, then you need to use a model that better describes your layer, perhaps a viscoelastic model, for layer characterization.
Download the overview to learn more about how the equation is derived and what the different parameters mean.
Editors note: This post was originally published in July 2018 and has been updated for comprehensiveness
Read the guidelines on how to decide which QCM instrument will be the most suitable for your needs
Read about what single-harmonic and multi-harmonic QCM-D means and what the difference is between these instruments.
Learn about the difference between the theoretical QCM sensitivity and the sensitivity which is relevant in a measurement situation.
Read about the piezoelectric effect and how piezoelectricity arises
QSense Omni is designed to offer cutting-edge QCM-D performance in modular setup-configurations based on user needs
To quantify the QCM mass you can use either the Sauerbrey equation or viscoelastic modelling. Learn what happens if you use the wrong approach.
Learn more about the different QCM:s and when to use which one.
QSense Omni is designed to minimize the user knowledge required to produce high-quality QCM-D data.
